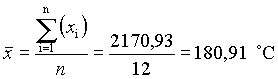
Az eutektikus hőmérséklet hibahatárainak számítása
Az Sn - Pb ötvözetek lehűlési görbéiből az alábbi eutektikus hőmérséklet adatokat határoztuk meg (°
C-ban):183,96; 183,56; 180,97; 182,25; 180,54; 180,45;
179,46; 181,00; 178,02; 180,00; 180,72; 180,00;
Adjuk meg az eutektikus hőmérséklet hibahatárait!
Először az adatok átlagát számítjuk ki:
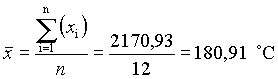
Az átlag korrigált tapasztalati szórása:
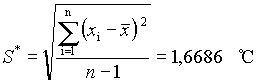
Az eredmény hibahatárainak megadásához 95%-os megbízhatósági szintet választunk (vagyis a tévedés valószínűsége 5%). Mivel 12 adatunk van, ezért az f=n-1=11 szabadsági fokhoz tartozó t kritikus értékkel számolunk:
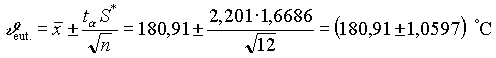
Az eredmény megadása:
vagy 
A hibahatárokat legfeljebb két értékes jegyre adjuk meg, az utolsó jegy kerekítésével. A szóbanforgó fizikai mennyiség értékes jegyeinek száma attól függ, mely helyiértéken jelentkezik a hiba. Ebben az esetben az egyes helyiérték már hibával terhelt, az ennél egg
yel kisebb helyiértéken lévő jegyet még megtarthatjuk kerekítéssel. Így kapjuk az eredményt.A fenti eredmény értelmezése: 95%-os biztonsággal állíthatjuk, hogy az eutektikus hőmérséklet valódi értéke a fent megadott intervallumban van.
A kiugró érték(ek) vizsgálata
A kiugró (extrém), adatok a számított középértéket és a szórást torzíthatják, ezért szükségessé válhat azok kizárása a további vizsgálatokból. Erre alkalmas pl. a Gauss-féle g-statisztika.
Kiszámítjuk az
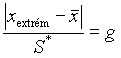
értékét, ahol xextrém a
„gyanús" kísérleti eredmény, 
a többi
adat átlaga a kiugró értéket figyelmen kívül hagyva. S*
Kiugró adat ellenőrzése:
A fenti eutektikus hőmérsékletek között szereplő 183,96 ° C -os adat tér el leginkább a többitől. Kérdés, figyelmen kívül hagyjuk-e mint kiugró értéket?
Kiszámítjuk az -ot és S* -ot a gyanús adatot figyelmen kívül hagyva.
A g-statisztika:
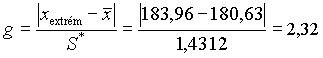
Mivel a számított g kisebb mint az n=12-höz tartozó táblázati g érték, ezért nem kell figyelmen kívül hagyni a kérdéses adatot.