A feladat során két galváncella elektromotoros erejének hőmérsékletfüggését mérjük és az így kapott adatokból számítjuk a cellareakcióra vonatkozó termodinamikai mennyiségeket. Itt csak az egyik cella adatait értékeljük és az illesztett egyenes paramétereit már ismertnek tekintjük.
1. táblázat
A 10-3 mol/dm3 Ag+ ion tartalmú galváncella elektromotoros erejének hőmérsékletfüggését kifejező adatok:
T / ° C |
EMF / V |
20,0 |
0,0240 |
22,5 |
0,0252 |
25,0 |
0,0266 |
27,5 |
0,0278 |
30,0 |
0,0289 |
32,5 |
0,0299 |
35,0 |
0,0310 |
37,5 |
0,0320 |
40,0 |
0,0330 |
42,5 |
0,0341 |
45,0 |
0,0352 |
47,5 |
0,0364 |
50,0 |
0,0375 |
Az illesztett egyenes egyenlete:
A szórások:
meredekség szórása
reziduális szórás:
Statisztikus
biztonságnak a 95%-ot választjuk, így 
, 
, 
.
A
regressziós egyenletből számított 
hibahatárai:
A konfidenciahatárok számítására vonatkozó összefügés:
ahol
Az Y szórásának számítása és az ahhoz szükséges segédmennyiségek képzése:
2. táblázat
x |
|
20,0 |
225,00 |
22,5 |
156,25 |
25,0 |
100,00 |
27,5 |
56,250 |
30,0 |
25,000 |
32,5 |
6,2500 |
35,0 |
0,0000 |
37,5 |
6,2500 |
40,0 |
25,000 |
42,5 |
56,250 |
45,0 |
100,0 |
47,5 |
156,25 |
50,0 |
225,00 |
S 455,0 |
S 1137,5 |
Az elektromotoros erő hibahatárai:
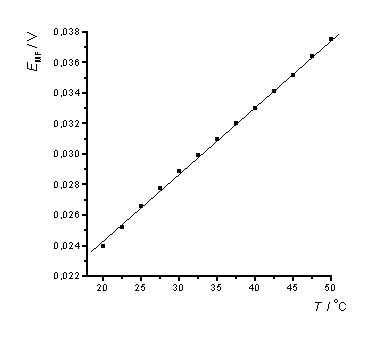
1. ábra
Galváncella elektromotoros erejének hőmérsékletfüggése
hibahatárainak
kiszámítása:
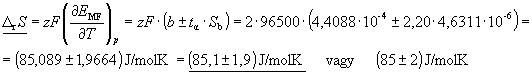
hibahatárainak
kiszámítása:
hibahatárainak
kiszámítása:
a termodinamikai mennyiség kiszámítása:
A hibahatárok
kiszámításához az 
és a 
konfidenciaintervallumát is be kell helyettesíteni a fenti
összefüggésbe:
Ez egy kissé bonyolultnak tűnik, de egyszerű a kifejtése.
Először behelyettesítjük mindkét konfidencia határt pozitív előjellel, majd negatívval, végül vegyesen. A vegyes behelyettesítésnél már csak összeadást vagy kivonást kell végezni, hiszen a szögletes zárójelben lévő mennyiségek az első két számítás után már ismertek.
1.
2.
3.
4.
A négy adat
közül kiválasztjuk a legnagyobb és legkisebb értéket, majd
ezeknek az eltérése az első lépésben számított 
-tól adja a
hibahatárokat:
legnagyobb: 
legkisebb: 
a hibahatárok: 
A 
hibahatárai:
a termodinamikai mennyiségkiszámítása:
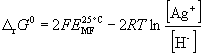
az elektromotoros erő hibahatárait is behelyettesítve:
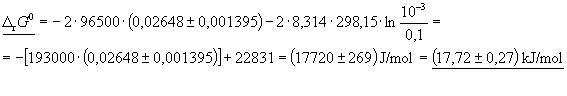
A szögletes
zárójelben lévő mennyiséget már a 
számításakor megadtuk, így most
kevesebb munkával kapjuk a végeredményt.
A többi termodinamikai mennyiség kiszámításánál a fentiekkel analóg módon járunk el.
A termodinamikai egyensúlyi állandó hibahatárai:
Mivel a 
, ahol 
a cellareakció
egyensúlyi állandója. Így a 
számítható a következő egyenlet
alapján:
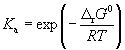
Itt három
lépésben kapjuk a hibahatárokat. Először a 
-t helyettesítjük be,
majd a hibahatárral növelt, illetve csökkentett értéket.
Ezzel három darab Ka -t kaptunk. A
hibahatárokat az elsőként kapott adathoz képest adjuk meg +
és - irányban.
innen a hibahatárok:
Amint az eredmény
mutatja nem szimetrikus hibahatárokat kapunk mint az
előzőekben, mert itt nemlineáris függvénnyel számolunk. A 
hibahatárainak
növekedésével nő ez az aszimmetria, csökkenésével pedig el
is tűnhet (legalábbis a hibahatár második jegyében már nem
jelentkezik).
