Reakciókinetika, elméleti összefoglalás.
A tapasztalatok szerint a kémiai reakciók ritkán mennek végbe úgy, ahogy azt a sztöchiometriai egyenlet alapján várnánk. A legtöbb átalakulás nem egyetlen reakciólépés eredménye, hanem több egyszerűbb, egymás után (sorosan) vagy egymás mellett (párhuzamosan) lezajló elemi folyamat eredőjének tekinthető. Ezeket az elemi folyamatokat nevezzük reakciólépéseknek.
Egy konkrét reakció esetében ezeknek az elemi lépéseknek az összességét nevezzük a reakció mechanizmusának, vagyis a mechanizmus megadásával leírjuk a reakció során lejátszódó részfolyamatokat, a fennálló egyensúlyokat, és megadjuk az esetleg képződő közti termékeket.A reakciókinetikai vizsgálatok elsődleges célja a folyamat sebességének megállapítása , illetve a folyamat időbeli lefolyását leíró izoterm bruttó sebességi egyenlet megalkotása. További cél lehet a reakció időbeli lefolyásának vizsgálatából és az esetleges közti termékek azonosítása során szerzett információk alapján a reakció mechanizmusán
ak megadása. A reakciók mechanizmusának felderítése, a katalizátorok erre gyakorolt hatásának ismerete elengedhetetlen egy vegyipari gyártási folyamat optimális vezetéséhez.A gyakorlatok során mi homogén és heterogén reakciókat egyaránt vizsgálni fogunk. A homogén re
akcióknál a folyamatban részt vevő anyagok, közti termékek és végtermékek ugyanabban a fázisban vannak jelen, és a reakció a fázis teljes térfogatában zajlik. A heterogén reakcióknál a folyamatban részt vevő anyagok különböző fázisban vannak jelen, és a reakció az érintkező fázisok határfelületén megy végbe. Előfordulhat az az eset is, hogy a reakciópartnerek és termékek ugyanabban a fázisban vannak, csak a reakció zajlik a határfelületen, pl. heterogén katalízis, egyes elektrokémiai reakciók stb.Ha vizsgálunk egy homogén reakciót, amely állandó térfogaton és hőmérsékleten irreverzibilisen és kvantitatíve játszódik le (köztitermékek felhalmozódása nélkül) a következő sztöchiometriai egyenlet szerint:
![]() (1)
(1)
akkor a reakciósebességet úgy is definiálhatjuk, mint a reakció partnerek vagy a termékek koncentrációjának időbeli változását:
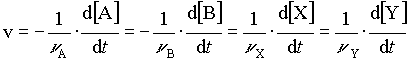 (2)
(2)
ahol [A], [B], [X], [Y] az A, B, X, Y anyagok pillanatnyi koncentrációit, a nA, nB, nC, nD az (1) egyenlet sztöchiometriai együtthatóit jelenti.
Szigorúan véve a reakciósebességet mint a reakciókoordináta változásának sebességét definiáljuk.
A![]() (3)
(3)
általános reakcióra a reakciókoordinátát a
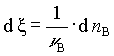 (4)
(4)
egyenlet definiálja, ahol nB a B anyagmennyisége, nB a sztöchiometriai száma. Az (1) egyenlettel összehasonlítva adódik, hogy 1 mol reakció megy végbe, ha a reakció egyenletben feltüntetett mennyiségű kiindulási anyagok végtermékekké alakulnak.
(A reakciókoordinátát hívják „reakció extenzitás"-nak is, hiszen azt fejezi ki,hogy milyen mértékben zajlott már le a reakció. A reakciókoorditánát nevezik még „reakciófok változónak” is, az angol nyelvű irodalomban használt elnevezés fordításaként. A reakciókoordináta számértéke a reakció kezdetén nulla, a reakció teljes lezajlása után 1, mértékegysége "mol" a (4)-nek megfelelően.)
A reakciósebesség:
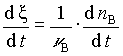 (5)
(5)
Ez a definíció független attól, hogy melyik komponenst választjuk B-nek, és milyenek a reakció körülmények. Ha a V térfogat állandó, akkor
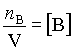
és következésképpen az (5) egyenletből
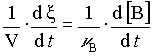 (6)
(6)
ahol az összefüggés jobb oldalán az általunk korábban használt sebességi definíció található. (A koncentrációváltozás sebességét térfogattal osztott reakciósebességnek is hívják.)
A továbbiakban reakciósebesség alatt a koncentrációváltozás sebességét értjük, azon egyszerű oknál fogva, hogy a gyakorlatban a koncentrációt tudjuk mérni, a reakciókoordinátát csak számítani.
A reakciókoordináta változásával definiált reakciósebesség dimenziója
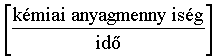 , mértékegysége:
, mértékegysége:  (7)
(7)
A koncentrációváltozás sebességének dimenziója
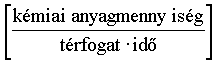 , mértékegysége:
, mértékegysége: 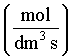 (8)
(8)
Mivel minden elemi reakciólépés csak úgy mehet végbe, hogy a megfelelőű energiájú komponensek érintkezésbe kerülnek egymással, a sikeres találkozások, ütközések valószínűsége, azaz a reakció ezzel arányos sebessége adott hőmérsékleten a reagáló anyagok pillanatnyi koncentrációjának a függvénye. A sebességi egyenlet ezen gondolatmenet alapján:
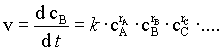
ahol k reakció sebességi együthatója (sebességi állandónak is hívják), és
![]()
a reakció rendűsége (bruttó rendűsége, kinetikai rendje) az rA, rB, rC
reakcióban résztvevő komponensekre vonatkozó részrend, cA, cB, cC az egyes reakciópartnerek pillanatnyi koncentrációja. A (9)-ben szereplő sebességi együtthatót és a részrendeket kísérletileg kell meghatározni!A fentieket általánosítva: a sebességi egyenlet olyan kísérletileg meghatározott egyenlet, amely a reakciósebesség és az összes reakcióban résztvevő molekula (részecske) pillanatnyi koncentrációja közötti összefüggést írja le.
Mivel a reakcióban résztvevő anyagok több reakciólépésnek is lehetnek kiindulási anyagai és végtermékei, a bruttó reakció kinetikai egyenlete nem mindig adható meg egyszerű módon az elemi lépésekre vonatkozó (9) típusú egyenletekből. Amennyiben a sebességi egyenlet nem írható fel a (9) egyenlet mintájára szorzat alakban, akkor a reakció bruttó rendűségéről sincs értelme beszélni.
A k sebességi együttható értéke adott reakció esetén független az időtől és a reakciórésztvevők koncentrációjától, függvénye a hőmérsékletnek (gázreakciók esetén a nyomásnak is) és a reakció közegének (oldószer minősége, egyéb komponensek koncentrációja stb.).
A sebességi együttható dimenziója a (9) alapján:
![]() (11)
(11)
Egy adott reakció esetén a rendet kísérletileg kell meghatározni, ezért a reakció rendűségét mindig szigorúan meg kell különböztetni a reakció molekularitásától. A reakció molekularitása ugyanis már a reakció mechanizmusával összefüggő fogalom, és azt mutatja meg, hogy az adott reakciólépés hány molekula kémiai kölcsönhatása során jön létre. Ebből nyilvánvaló, hogy molekularitásról valójában csakis elemi reakciók esetében beszélhetünk.
A reakciókinetikai vizsgálatok során általában három feladatcsoporttal kell foglalkozni:
- az izoterm bruttó sebességi egyenlet megalkotása (a sebességi együttható és a
részrendek meghatározása);
- a sebességi egyenlettel összhangban lévő mechanizmus felírása (megtalálása);
- a sebességi állandó hőmérsékletfüggésének meghatározása és annak értelmezése.
Az izoterm bruttó sebességi egyenlet megalkotása
Ha egy reakció sebességi egyenletét a mérési adatokból akarjuk meghatározni, két lényeges feladat adódik:
a) a reakciórendűség meghatározása a reakcióban résztvevő összes anyagra;
b) a k reakciósebességi együttható számszerü értékének meghatározása.
Egy reakció sebességi egyenletének meghatározásához először is az szükséges, hogy valamilyen analitikai módszerrel kövessük a reakció előrehaladását az időben. Ennek a megoldása lényegesen egyszerűbb, ha a reakció sztöchiometriája pontosan ismert, és a reakció kvantitatív, (tehát irreverzibilisen és mellékreakciók nélkül), valamint közti termékek képződése nélkül megy végbe. Ilyenkor elegendő csak az egyik reakciópartner fogyását vagy képződését követni, hiszen a sztöchiometriai egyenlet alapján számítható a többi reakciópartner fogyása, ill. képződése is. Összetett reakciók esetén azonban a rendszer összetételének ismeretéhez több reagáló partner időben bekövetkező koncentrációváltozásának egyidejű ismerete szükséges.
A sebességi egyenlet meghatározásának egyik módja az ún. pszeudo zérusrend módszere.
Lényege, hogy ahhoz a reaktánshoz képest, amelynek a koncentrációját követjük, a többit nagy feleslegben alkalmazzuk, így ezeknek a reaktánsoknak a koncentrációja időben nem változik, ezekre nézve nulladrendű a reakció. A kinetikai egyenlet egyszerűsödik, a sebesség függése az egyes reaktánsok koncentrációjától egyenként meghatározható, és a teljes sebességi egyenlet kikövetkeztethető.A kezdeti sebességek módszere, amelyet gyakran a pszeudo zérusrendek
módszerével kombinálva alkalmaznak, a reakciók kezdeti sebességének különböző kiindulási koncentrációk mellett történő meghatározásán alapszik. Ezzel a módszerrel nem határozhatjuk meg a teljes sebességi egyenletet, mert egy összetett reakcióban a termékek is befolyásolhatják a sebességet.Ahhoz, hogy a koncentráció idő szerinti változásából (kinetikai görbe) meghatározhassuk a rendet és a sebességi állandót, a sebességi egyenleteket integrálni kell. Erről tájékoztat a 1. táblázat. Olyan integrált sebe
sségi egyenletet kell találnunk amely a legjobban közelíti a mért koncentráció - idő függvényeket. Ennek van egy hagyományos („klasszikus”) módszere, és lehetséges a paraméterbecslés alkalmazása is.Egyszerű reakciók esetében célszerü megnézni, hogy a 1. táblázat integrált sebességi egyenletei közül melyik illeszkedik legjobban a mérési adatokhoz. Ezt megtehetjük grafikusan vagy számítással. A grafikus módszer esetén átalakítjuk (linearizáljuk) a szóbanforgó sebességi egyenleteket. Ezután a lineáris kapcsolatot adó koncentráció kifejezést ábrázoljuk a reakcióidő függvényében, és megnézzük, mely sebességi egyenlet alapján adódik egyenes. Az egyenes iránytangenséből (meredekségéből) kiszámítható a sebességi állandó. Az integrált sebességi egyenletek érvényességének számítással történő ellenőrzése során az összetartozó koncentráció és idő adatpárokat az egyenletekbe behelyettesítve kiszámítjuk k értékeit. Ha a k kiszámított értékei nem mutatnak az időtől való rendszeres függést, hanem véletlenszerüen ingadoznak egy átlagérték körül, akkor a vizsgált egyenlet megfelelő. Persze a rendűség megállapítására vannak egyszerűbb módszerek is (lásd az ajánlott irodalmat). Azonban ezeknél a módszereknél is a koncentráció - idő összefüggésekkel van dolgunk, hiszen a reakciók vizsgálatánál minden esetben a koncentráció (vagy vele arányos más fizikai mennyiség) változását követjük az időben.
A paraméterbecslésnél a kísérletileg mért koncentráció - idő függvényeket hasonlítjuk össze a feltételezett sebességi egyenletből számított koncentráció - idő függvényekkel. A sebességi egyenletben szereplő sebességi együttható és részrend értékeit úgy határozzuk meg, hogy a lehető legkisebb legyen az eltérés a mért és a számított koncentráció - idő függvények között. A sebességi egyenletnek természetesen összhangban kell lenni a reakció feltételezett mechanizmusával. Vagyis a paraméterbecslés csak technikai segédeszköz, nem helyettesíti a szigorú szakmai megfontolásokat.
1. táblázat
SEBESSÉGI EGYENLETEK
|
reakciórend |
differenciálegyenlet |
integrált sebességi |
felezési idő t1/2 |
k mértékegysége |
||
|
r |
a |
b |
egyenlet |
|||
|
0 |
0 |
0 |
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
2 |
2 |
0 |
|
|
|
|
|
2 |
1 |
1 |
|
|
|
|
r
bruttó rend;a, b részrendek;
a, b sztöchiometriai együtthatók; (az előzőekben n A, n B)
k sebességi együttható;
A, B pillanatnyi koncentrációk;
A0, B0 kezdeti koncentrációk.
A reakciósebességi együttható meghatározása
A laborgyakorlatokon végzett reakciókinetikai mérésekben szereplő reakciók esetében érvényes integrált sebességi egyenlet linearizált alakjába helyettesíjük az idő–
koncentráció értékpárokat, és a kiértékelést többnyire grafikusan végezzük (a konkrét megoldást lásd az adott méréseknél).A reakciósebesség hőmérsékletfüggése, aktiválási energia számítása
Általános tapasztalat, hogy a homogén kémiai reakciók egy részé
nek sebesssége növekszik a hőmérséklet növekedésével. Kísérleti vizsgálatok alapján állította fel Arrhenius a következő összefüggést: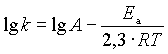 (12)
(12)
ahol k a reakció sebességi együtthatója, A az ún. preexponenciális együtható, (értelmezésével a reakciósebességi elméletek foglalkoznak), Ea-t pedig aktiválási energiának hívjuk. A (12
) összefüggés csak szűk hömérséklet intervallumban érvényes, mert A és Ea egyaránt függhetnek a hőmérséklettől. (A laborgyakorlatokon vizsgált reakciók esetében 40–50 fok intervallumban állandónak tekinthető A és Ea.) A (12) összefüggés csak akkor érvényes, ha a folyamat egyszerű és termikus aktiválású.Robbanásoknál, katalitikus vagy enzimreakciókban és egyébb összetett folyamatoknál (pl. soros, párhuzamos folyamatok; egyensúlyok) a fenti egyenlettől eltérő hőmérsékletfüggés is tapasztalható. Előfordul, hogy a reakciósebesség csökken a hőmérséklet emelkedésével, esetleg maximumon megy át, stb.
Az Arrhenius-összefüggés egyenes egyenletének felel meg. Ha 1/T függvényében ábrázoljuk a sebességi együtthatók logaritmusát, a kapott e
gyenes meredekségéből (m) számítható az Ea aktiválási energia.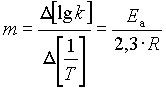 (13)
(13)
Az aktiválási energia:
![]() (14)
(14)
![]()
Természetesen a legkisebb négyze
tek módszerével illesztett egyenes meredekségéből számítjuk az aktiválási energiát.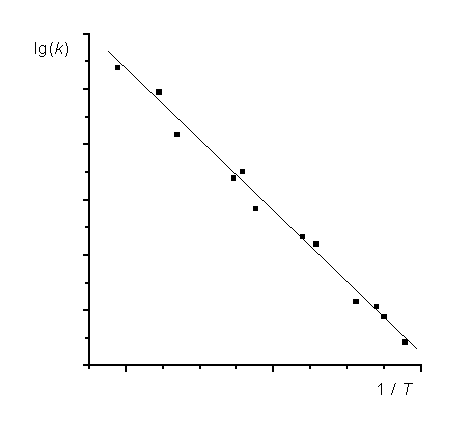
1. ábra
Az Arrhenius összefüggés képe az aktiválási energia számításához
A reakciókinetikai vizsgálatokhoz alkalmazható kísérleti módszerek (a reakciók követése az
időben)Bármilyen reakciókinetikai mennyiség meghatározása feltételezi a reakciók időbeli követését. A reakciók időbeli követése mindig egy vagy több kiindulási anyag vagy termék koncentrációjának mérését jelenti. Ez megoldható időnkénti mintavétellel
és elemzéssel vagy az egész rendszer egy vagy több fizikai kémiai tulajdonságának folyamatos mérése útján.Mintavételes követés
A reakcióelegyből különböző időpontokban kivett mintát megfelelő analitikai módszerekkel elemezzük (ez lehet akár hagyományos kémiai analízis is, pl. titrálás). Fontos, hogy az analízis a reakcióidőhöz képest gyorsan elvégezhető legyen, mert a minta nem reagálhat tovább az analízis elvégzéséig. A reakciót a kivett mintában leállíthatjuk, pl. a minta gyors lehűtésével, vagy va
lamilyen reagens adagolásával (a reakció befagyasztása). A mintavételes eljárás alkalmas olyan reakciók követésére, amelyek vizes oldatban játszódnak le szobahőmérséklet közelében. Ha a gyakori mintavétel miatt bekövetkező térfogatváltozások hatással vannak a reakció további lefolyására, ez a módszer nem alkalmazható.Folyamatos követés
A fizikai analitikai módszerek
közül sok igen gyors és nem zavarja a reagáló rendszert. Ezért a mérések közvetlenül a reakciótérben is végezhetők, a mintavétel feleslegessé válik. A reakciók követésére minden olyan fizikai tulajdonság alkalmas, amely a reakció lezajlása során jól mérhetően megváltozik, és valamilyen módon egyértelmű kapcsolatba hozható a reakció partnerek vagy termékek koncentrációjával. Ha a mért fizikai mennyiséget egyetlen anyag koncentrációja határozza meg, akkor kalibrációs görbe segítségével egyértelműen megadható a mért fizikai mennyiség és az illető vegyület koncentrációjának kapcsolata. Ilyenkor a reakciókinetikai vizsgálatok során mért mennyiségeket közvetlenül koncentrációértékekké lehet átszámítani, amelyek már alkalmasak k meghatározására.A legtöbb fizikai módszer esetében a közvetlenül mért fizikai mennyiség - pl. elektromos vezetés, térfogat, vagy az összes nyomás-
nem jellemző egy konkrét vegyületre, hanem a rendszer valamennyi komponensének jellemzőiből adódik össze. Általában (híg oldatokban), ezeknek az adatoknak a nagysága arányos a komponensek koncentrációjával; példaként lásd az észterek elszappanosodási reakcióját.A térfogatmérés
a térfogat-változással járó gázreakcióknál vagy olyan reakcióknál alkalmazható, amelyek gázfejlődéssel vagy gázelnyeléssel járnak. Ilyen esetekben különösen fontos, hogy a hőmérséklet mellett a nyomást is állandó értéken tartsuk. Ha a reakció folyadékfázisban megy végbe gázfejlődés mellett, akkor fontos, hogy a gáz a folyadékkal egyensúlyban legyen.Ha a gázreakcióban a sztöchimetriai szám megváltozása nem nulla, - és állandó térfogaton játszatjuk le a folyamatot- akkor követésére jól alkalmazható az össznyomás változásának mérése.
Az optikai tulajdonságok közül a törésmutató, a fényabszopció és az optikai forgatás mérése alkalmas a reakciók követésére. Mivel a törésmutató változása általában igen kis mértékü, ezért azt inte
rferométerrel célszerű mérni.A fényabszorpció
spektrofotométerrel vagy koloriméterrel mérhető. Ha a reakcióban részt vevő anyagok közül csak egy színes, akkor elegendő egy hullámhosszon végezni a mérést. Ha több színes anyag van a reakcióelegyben, akkor vagy több hullámhosszon kell mérni, vagy az előzetesen felvett abszorpciós görbékből meghatározható egy olyan hullámhossz, amelyen a színes anyagok közül csak az egyik abszorbeál.Ha a reakcióban részt vevő anyagok, vagy a reakciótermékek egyike opt
ikailag aktív, akkor a reakciót az optikai forgatás mérésével lehet követni.Az elektromos vezetés mérése
akkor alkalmas a reakciók követésére, ha az oldatreakció során az ionok koncentrációjában vagy minőségében következik be változás. Különösen érzékeny a mérés, ha az egyik reakciópartner vizes közegben szolvatált OH-- vagy H3O+- ion. A vezetés konduktométerrel mérhető.A koncentrációváltozás elektromotoros erő mérésével is követhető, ha valamelyik reakciópar
tnerre nézve reverzibilis elektródot tudunk készíteni.Az elektródokon stacionárius állapotban lejátszódó heterogén elektrokémiai reakciók tanulmányozása az elektródpotenciál és az elektródon átfolyó áram kapcsolatát kifejező
polarizációs görbe vizsgálatával lehetséges.A reakcióelegy összetevőinek gyors elválasztására, minőségi és mennyiségi meghatározására egyaránt alakalmasak a
kromatográfiás módszerek.Gyors reakciók követése
A fenti kísérleti módszerek csak olyan reakciók kinetikai vizsgálatára alkalmasak, amelyek felezési ideje nagyobb 10 s -nál.
Az ún. áramlásos technika
alkalmazásakor a reaktánsok folytonos áramát egy keverőkamrában egyesítik, ami egy csőben folytatódik. A cső különböző helyein (más-más távolságban a keverőkamrától) mérve a koncentrációkat (pl. spektrofotometriásan), ugyanarra az eredményre jutunk, mintha az összekeveréstől eltelt idő függvényében vizsgálnánk a reakciót. Ezzel a módszerrel az 1 s felezési idejű reakciók is tanulmányozhatók. Az áramlásos technikák hátránya, hogy nagy mennyiségű oldatokat igényelnek, hiszen a megfelelő felbontás érdekében nagyra kell választani az áramlási sebességet.A megállított áramlás módszerénél
a két oldatot gyorsan mozgó fecskendőkkel juttatják be egy keverőkamrába, amelynek a kiképzése tökéletes keveredést biztosít. A keverőkamra után egy küvetta, majd egy ellenkező irányba mozgó dugattyújú fecskendő van, melyet az áramló oldat egy ütközőig mozgat. Ez megállítja az áramlást, és elindítja a számítógép vezérelt adatgyűjtést. A küvettában zajló reakciót többnyire spektrofotometriásan követjük. E módszer különösen alkalmas biokémiai reakciók tanulmányozására, mert oldatigénye kicsi. Felfedezése óta az enzimreakciók vizsgálatának nélkülözhetetlen eszköze.