Az EMF, a kapocsfeszültség és a galváncella belső ellenállása
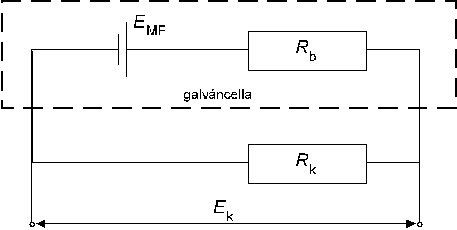
Egy galváncella feszültségének mérése méréstechnikai szempontból az alábbi egyszerű elektromos kapcsolással reprezentálható:
1. ábra
Kapocsfeszültség mérése
A körben folyó áram Ohm törvénye szerint:
A galváncella pólusai) között mérhető feszültség, - ami az Rk külső ellenálláson esik - szintén az Ohm-törvényből számítható:
Az egyenlet átrendezésével:
(1)
Ebből az összefüggésből látható, hogy a kapocsfeszültség mindig kisebb az elektromotoros erőnél, de azt annál jobban megközelíti, minél kisebb Rb, és minél nagyobb Rk. Határesetben Rk®¥, Ek®EMF. Ez azt is jelenti, hogy a cellán átfolyó áram nullához tart.
Itt lehetőség kínálkozik az elektromotoros erő meghatározására abban az esetben is, ha nincs olyan nagy bemenő ellenállású feszültségmérőnk, ami nem terheli le a galváncellát. A megoldás, hogy különböző Rk külső ellenállásokkal terheljük a galváncellát, és mérjük az ezekhez tartozó kapocsfeszültségeket. Ezután a cellán átfolyó áram függvényében ábrázoljuk a kapocsfeszültséget, és nulla áramra extrapolálva kapjuk az elektromotoros erőt.
A kapocsfeszültség annyival kisebb az elektromotoros erőnél, amekkora feszültség a cella belső ellenállásán esik:
Az áram Ohm törvényéből:
.
Ezt behelyettesítve
(2)
A (2) összefüggés egy egyenes egyenlete. Ha az Ek-t az Ek/Rk függvényében ábrázoljuk, egyenest kapunk, amelynek tengelymetszete az elektromotoros erő, iránytangenséből pedig az Rb-t kapjuk. (Megjegyzés: a (1) és (2) összefüggés teljesen egyenértékű, egymásba átalakítható.)
Az elektromotoros erő mérése kompenzációval
Az elektromotoros erő kompenzációs mérési elvét a 2. ábra szemlélteti. Az Uk kompenzációs feszültségforrás az R1 és R2 ellenállásokon Ik=Uk/(R1 + R2) kompenzációs áramot állít be. Amennyiben gondoskodunk arról, hogy Uk stabil és R1+R2 állandó legyen, akkor Ik állandó marad a mérés folyamán. Az R1 ellenállásra csatlakoztatjuk a mérendő galváncellát a K kapcsolón és a G galvanométeren keresztül. (A galvanométer egy nagy érzékenységű árammérő.)
Az R1 ellenállást úgy állítjuk be, hogy a galvanométer árammentes állapotot jelezzen. (Ha R1-et csökkentjük, akkor R2-t növelni kell, hogy összegük állandó maradjon). Ekkor az Ik kompenzációs áram által az R1 ellenálláson létrehozott feszültség egyenlő lesz a mérendő elektromotoros erővel:
.
Amikor a normálelemet csatlakoztatjuk, és az R1 változtatásával megvalósítjuk az árammentes állapotot, akkor:
.
E két egyenletet osztva egymással, kiszámíthatjuk Ex-et.
(3)
A K kapcsolót csak rövid időtartamokra zárjuk, amíg ellenőrizzük az árammentes állapotot, így elkerülhető az elektródok polarizációja.
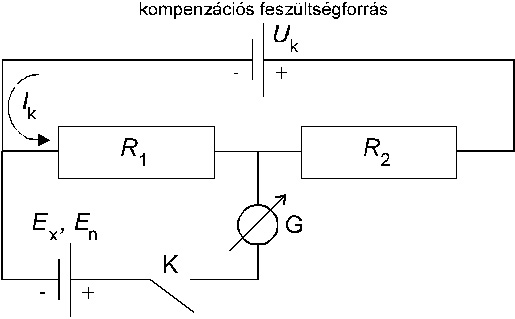
2. ábra
A kompenzációs
mérés elve
Mérőberendezés
A 3. ábrán vázolt megoldásnak megfelelően két változtatható ellenállásszekrényt alkalmazunk. A mérés kezdetén a bal oldali ellenállást (ahova a mérendő, illetve a normálelem csatlakozik) beállítjuk a maximális értékre, a jobb oldalit nullára. A kompenzáció során amennyivel csökkentjük az R1-et, annyival kell növelni az R2-t, és fordítva. A kikompenzált állapotnak megfelelő Rx és Rn értékeket a (3) egyenletbe helyettesítve kapjuk Ex-et.
A kompenzációs mérőeszköz gyakorlati megvalósítására egy egyszerűsített megoldást is alkalmazhatunk: a változtatható ellenállások helyett homogén keresztmetszetű ellenálláshuzalt használunk. Ehhez egy csúszó érintkező csatlakozik, amellyel változtathatjuk R1 és R2 arányát úgy, hogy az összegük állandó marad. Mivel az egyenletes keresztmetszetű huzal ellenállása egyenesen arányos a hosszával, ezért ellenállás helyett hosszúságegységekkel is számolhatunk. Amennyiben az ellenálláshuzalt feltekert formában használjuk - potenciométernek hívják az így elkészített eszközt - , akkor a skálán leolvasott osztásrészt is behelyettesíthetjük az (3) egyenletbe.
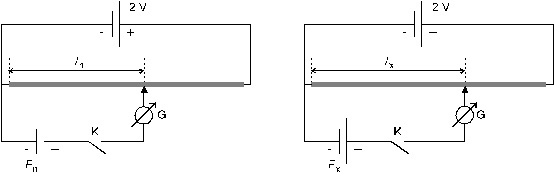
3. ábra
A kompenzációs EMF mérés gyakorlati megvalósítása
Kis és nagy belső ellenállású Daniell-cella vizsgálata, EMF és kapocsfeszültség mérése, az EMF koncentrációfüggésének vizsgálata
A galváncella
Az általunk vizsgált galváncella celladiagramja:
(-) Cu(s) | Zn (s) || 0,1 M ZnSO4 ¦ áramkulcs telített KNO3 -oldat ¦ 0,1 M CuSO4 || Cu (s) (+) (4)
1. A galváncella összeállítása
Az üvegből készült csapos elektródedényekből sóhíd közbeiktatásával összeállítjuk a Daniell-cellát. Az elektródedények csatlakozó csöveit buborékmentesen kell megtölteni A csapok csiszolatait meg kell nedvesíteni a betöltött elektrolittal a vezetés biztosítására. A csapokat bezsírozni szigorúan tilos! Az elektródok felületét alaposan csiszoljuk meg csiszolópapírral. Figyeljünk arra, hogy a csiszolópapírokat ne keverjük össze: a Cu-elektród megcsiszolására csak a rézelektródhoz tartozó üvegből kivett csiszolópapírt alkalmazhatjuk, s a csiszolópapírt használat után ugyanoda kell visszatenni! Értelemszerűen ugyanez áll a Zn-elektródra is.
2. EMF és kapocsfeszültség mérése
Megmérjük az összeállított galváncella elektromotoros erejét a nagy bemenő ellenállású feszültségmérővel, és az adatot rögzítjük a jegyzőkönyvben. A vizsgálandó Daniell-elemre ismert ellenállásokat (Rk) csatlakoztatunk, és nagy bemenő ellenállású feszültségmérővel megmérjük a kapocsfeszültséget. A nagyobb ellenállásoktól a kisebbek felé haladva végezzük a mérést. Az adatokat táblázatosan rögzítjük. A mérési sorozatot végrehajtjuk nyitott, majd zárt csapállásnál. Nyitott csapállásnál kisebb belső ellenállású, zárt csapnál nagyobb belső ellenállású galváncellánk lesz. Adott mérési sorozat közben ne váltogassuk a csapok állását, mert ettől változik az Rb értéke.
3. EMF mérése kompenzációval
Először a vizsgálandó cellával, majd a normálelemmel is összeállítjuk a kompenzációs áramkört (3. ábra). A kompenzációs áramkörben az ellenállások arányának (az összeg állandó marad!) változtatásával létrehozzuk a kikompenzált (árammentes) állapotot. A kompenzált állapotnak megfelelő lx és ln, (illetve osztásrész) értékeket feljegyezzük.
A K kapcsolót a mérés folyamán csak pillanatokig zárjuk, amíg a mérőkör árammentes állapotát ellenőrizzük (ezzel elkerülhető az elektródok polarizációja). Az elektródedények csapjait nyitva tartjuk.
4. Az EMF koncentrációfüggésének vizsgálata
Az eredeti 0,1
mol/dm3 koncentrációjú CuSO4-oldatból 4 higítást készítünk
a 0,1 és 0,001 mol/dm3 koncentrációintervallumban, úgy, hogy a
logaritmikus skálán nagyjából egyenlő közű (ekvidisztáns) legyen az osztás.
Az állandó ionerősség biztosítására a hígitást nem desztillált vízzel, hanem
0,1 mol/dm3 koncentrációjú MgSO4-oldattal végezzük (az állandó ionerősséggel
biztosítjuk a 
állandó értékét).
Valamennyi oldattal összeállítjuk a kalomel elektród¦Cu2+|Cu galváncellát,
és megmérjük az EMF-t
nagy bemenő ellenállású digitális voltmérővel. Így öt adatpárunk lesz. A 0,1 mol/dm3
-os CuSO4-oldattal már a mérés elején elkészítettük az elektródot,
most megmérjük az elektródpotenciált a kalomelelektródhoz képest. Ezután
a rézelektródot alaposan leöblítjük desztillált vízzel, majd az 0,001 mol/dm3-os
CuSO4-oldattal, és az elektródedénybe is ezt az oldatot töltjük.
3 - 4 perc várakozás után feljegyezzük az összeállított galváncella EMF-jét.
A további méréseket a töményebb oldatok felé haladva végezzük, mert így elkerülhető,
hogy a réz felületén adszorbeálódott Cu2+-ionok
meghamisítsák az eredményeket.
Az adatok rögzítésére javasolt táblázat:
|
|
|
|
1. A kapocsfeszültség-mérés adatainak értékelése
A (2) egyenletnek megfelelően az Ek adatokat ábrázoljuk az Ek/Rk függvényében. A pontokra egyenest illesztünk a legkisebb négyzetek módszerével. Ebből megkapjuk az EMF-t és a cella belső ellenállását. Ezt az értékelést egyaránt elvégezzük a nyitott és zárt csapállásoknál kapott adatokra.
2. A kompenzációs mérés adatainak kiértékelése
A fent levezetett összefüggések alapján az elektromotoros erő:
(5)
3. A koncentrációfüggés kiértékelése
A kalomelelektród¦Cu2+|Cu galváncella EMF adatait ábrázoljuk Cu2+-koncentráció logaritmusának függvényében (Nernst-egyenlet). A pontokra egyenest illesztünk a legkisebb négyzetek módszerével. Az egyenes két paramétere megfelel a Nernst-egyenletben szereplő állandóknak.
4. A galváncella maximális munkája
A galváncella által végezhető maximális munkát a DrG = - zFEcell öszszefüggésből számítjuk ki. DrG értéke akkor lesz maximális, ha az elektromotoros erővel számolunk, vagyis a galváncellában lejátszódó folyamatok reverzibilis lefolyását tételezzük fel. A Daniell-cellánál a nagy bemenő ellenállású feszültségmérővel mért EMF adatot helyettesítsük be!
5. A hibahatárokat a mintapélda alapján határozzuk meg.
Beadandó:
