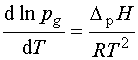Egy heterogén rendszerben akkor áll fenn egyensúly, ha a nyomás és a hőmérséklet a rendszer minden pontján ugyanakkora, és az egyes komponensek kémiai potenciálja minden fázisban ugyanakkora (de a különböző komponensek kémiai potenciálja egymástól természetesen általában különböző).

Az egykomponensű, kétfázisú heterogén rendszerekre elméleti és gyakorlati szempontból egyaránt fontos példa a tiszta folyadék és telített gőzének egyensúlya. A fázistörvény szerint ennek a rendszernek egy szabadsági foka van, azaz adott hőmérsékleten a folyadék gőze csak egyetlen nyomáson van egyensúlyban a cseppfolyós fázissal (gőznyomás, tenzíó), vagy egy adott gőznyomáshoz csak egyetlen egyensúlyi hőmérséklet tartozik. Az egyensúlyi gőznyomásnak a hőmérséklettel való változását, vagyis a gőznyomásgörbét közelítőleg a Clausius-Clapeyron-egyenlet írja le:

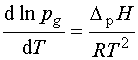     (1)

ahol p_g a telített gőz nyomása, D_pH pedig a folyadék moláris egyensúlyi párolgáshője.

A Clausius-Clapeyron-egyenletnek kis hőmérséklet-intervallumban való integrálásával (ha D_pH a hőmérséklettől független) a következő egyenlethez jutunk:

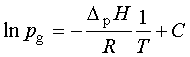     (2)

ahol C az integrációs állandó.

Az integrációs állandó ismeretére nincs szükség, ha két hőmérsékleten meghatározzuk a gőznyomást, és az így kapott két egyenletet kivonjuk egymásból.

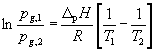     (3)

Ennek az egyenletnek az alapján kiszámíthatjuk az egyensúlyi párolgáshőt, ha két hőmérsékleten megmértük a gőznyomást. Pontosabb eredményhez jutunk, ha több hőmérsékleten mérjük meg a gőznyomást, és a mérési adatok alapján megrajzoljuk az ln p_g = f(T^-1) függvényt, ami a (2) egyenlet alapján egyenes. Ennek az egyenesnek az iránytangenséből kiszámítható a vizsgált hőmérséklet-tartományhoz tartozó közepes moláris egyensúlyi párolgáshő. Ennek ismeretében a vizsgált hőmérséklet-tartományban egy kiválasztott hőmérsékleten kiszámítható az egyensúlyi párolgási entrópiaváltozás a

     (4)

összefüggés alapján.

A gőznyomás meghatározására szolgáló módszerek egyike, a sztatikus módszer mellett, a dinamikus vagy Ramsey-Young módszer. A dinamikus gőznyomás meghatározás lényegében véve a sztatikus módszer fordítottja. Az eljárás lényege az, hogy beállított, adott nyomásnak megfelelő egyensúlyi hőmérsékletet, azaz forráspontot határozunk meg. Előnye, hogy e módszerrel nemcsak az össznyomás, hanem több komponensű gőzben a parciális nyomások is meghatározhatók. Az erre a célra alkalmas berendezés rajza az 1. ábrán látható.

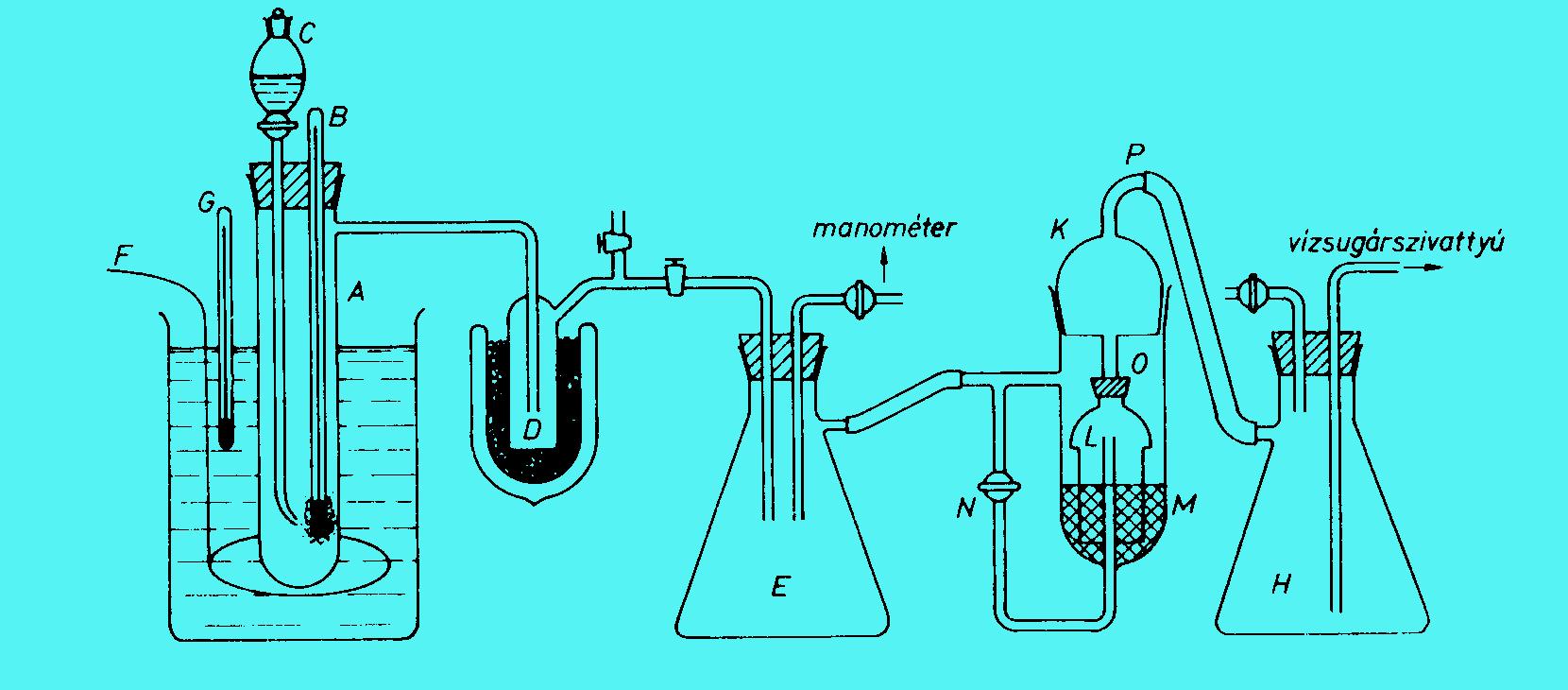
1. ábra

A-nagy kémcső, B és G-hőmérők, C-kihúzott végű rázótölcsér, F keverő, D-csapda, E, H pufferpalackok, K-Cartesius-manosztát, L-úszó, M-külső edény, N-csap, O-gumidugó, P-vákuumvezeték

Meghatározandó a víz-gőz rendszer egyensúlyi hőmérséklete öt nyomáson, valamint a víz moláris egyensúlyi párolgáshője a mért hőmérséklet-tartományban.

Felhasznált anyagok

Desztillált víz, darált jég.

Mérési eszközök:

Ramsay-Young-gőznyomásmérő berendezés (1. ábra), Cartesius-manosztát (lásd az itt jelölt segédanyagot), vízsugárszivattyú, 2 db pufferpalack, Bunsen-égő, vas háromláb, azbesztháló.

A mérés kivitelezése:

A hőmérőre csavart vattának az a célja (1. ábra), hogy a folyadék nagy felületen oszoljék szét, így a túlhevülés veszélyét elkerüljük. A vattarétegre a C rázótölcsérrel állandóan friss vizet juttatunk olyan sebességgel, hogy a vattaréteg állandóan nedves legyen, de a folyadék ne gyűljön össze a kémcső alján. A termoszpalackba jeget teszünk és belemerítjük a D csapdát. A nagy hengerpoharat megtöltjük vízzel és mikrolánggal lassan melegítjük. Ezután a manosztát segítségével a rendszerben egy adott, pl. 130 · 10² Pa nyomást állítunk elö.

Ha a kívánt nyomást beállítottuk, a nagy hengerpohárban levö vizet kb. 5 °C-kal e nyomáshoz tartozó forráshőmérséklet fölé melegítjük. Ezt a hömérsékletet az 1. táblázatról olvashatjuk le.

1.táblázat

A víz gőznyomásának hőmérsékletfüggése.

A vattarétegre jutott víz párolog, ezáltal hőmérséklete csökken. Az elpárolgó vízgőz a D csapdában kondenzál. Párolgás közben a víz hőmérséklete mindaddig csökken, amíg a rendszerben levö össznyomással egyenlő gőznyomáshoz tartozó egyensúlyi hőmérsékletet el nern éri. Az akkor leolvasott hőmérséklet megfelel a manométeren leolvasott nyomáshoz tartozó forráshőmérsékletnek. A párolgáshoz szükséges hőt a nagy főzőpohárban levő meleg víz hője fedezi. E külső temperálás azért is fontos, hogy szobahőmérsékleten a nagy kémcsőben ne kondenzálódjon a gőz, mert ebben az esetben a kondenzálódott víz újbóli elpárolgása megváltoztatná az adott nyomáshoz tartozó egyensúlyt. .

A nyomás és a hozzá tartozó fürdőhőmérséklet beállítása után pár perc múlva a hőmérőt addig olvassuk le egyperces időközökben, amíg a leolvasott hőmérséklet a kísérleti hibák határán belül (± 1 °C) állandóvá nem válik. Ezután leolvassuk a barométer és a manométer állását, és feljegyezzük azok hőmérsékletét is, hogy a mindkét nyomást 0 °C-ra redukálhassuk (ld. (5)-(6) egyenleteket alább). A készülékben levő nyomást megkapjuk, ha a 0 °C-ra redukált barométerállásból levonjuk a manométeren leolvasott és 0 °C-ra redukált nívókülönbséget. A forráshőmérsékletet mérjük meg még legalább négy különböző nyomáson (pl. 20, 30, 40, 50 kPa).

A mérés kiértékelése

Ha a manométeren leovasott nyomást mm-ben mérjük és a Hg hőtágulását figyelembe vevő

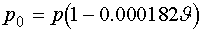     (5)

összefüggés (papírskála-korrekció) alapján 0 °C-ra redukáljuk, akkor a nyomást mmHg egységben kapjuk meg. Az (5) egyenletben J a szobahőmérséklet °C-ban.

A leolvasott légnyomást a Hg és a skála hőtágulását figyelembe vevő

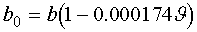     (6)

összefüggés (rézskála-korrekció) alapján redukálhatjuk 0 °C-ra. A (6) egyenletben J a szobahőmérséklet abban a helyiségben, ahol a barométer van. A két redukált nyomásérték különbsége megadja a gőznyomást a fürdő hőmérsékletén.

Ábrázoljuk az egyensúlyi gőznyomást a hőmérséklet függvényében, valamint a gőznyomás logaritmusát a hőmérséklet reciprokának függvényében ! Az utóbbi görbe felhasználásával számítsuk ki a víz moláris egyensúlyi párolgáshőjét, és adjuk meg J/mol egységben ! Számítsuk ki az víz moláris párolgási entrópiaváltozását a vizsgált hőmérséklettartomány közepén J/(mol K) egységben ! Végezzünk hibaszámítást mindkét mennyiségre vonatkozóan !

Beadandó: